Period Of A Cot Function
Ray is a licensed engineer in the Philippines. He loves to write about mathematics and civil engineering.

This article volition innovate you to the cotangent function and how to graph information technology.
Aaron Lefler/Unsplash
What Is a Cotangent Office?
Cotangent is the reciprocal of the tangent role. It is an odd function defined past the reciprocal identity cot (x) = 1 / tan (x). The cotangent graph can exist sketched by start sketching the graph of y = tan (x) and so estimating the reciprocal of tan (x). It has the aforementioned period every bit its reciprocal, the tangent function.
A cotangent graph is a discontinuous graph that is non defined for theta values such that the value of sin (θ) is equal to zero. You lot can observe from the sin graph that the cotangent part has vertical asymptotes at the zero values of the sine graph.
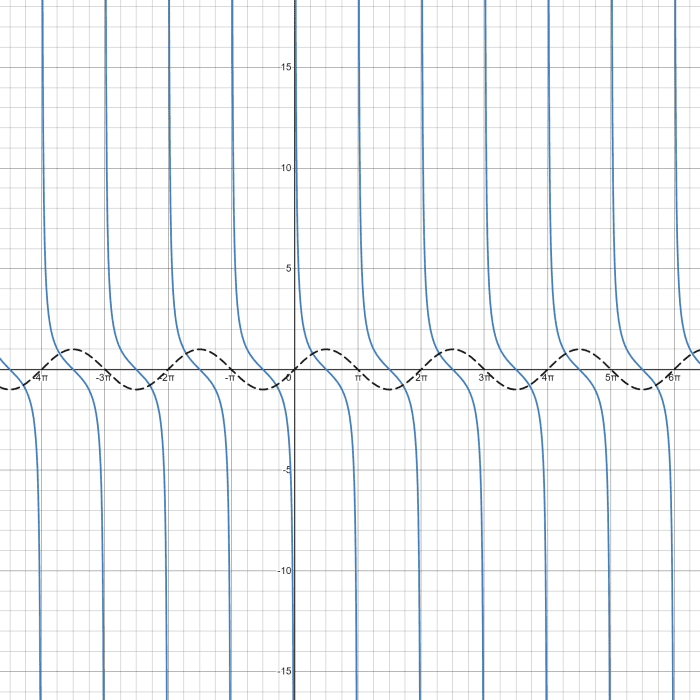
Cotangent Graph and Sin Graph
Cotangent Graph Backdrop
Aamplitude
The amplitude of cotangent is not defined. Since relative values of x for which the cotangent is not specified, they are unbounded. The graph of cotangent functions goes on unending in the vertical direction. For y = α cot (βx - c) + d, the amplitude, sometimes called the stretching factor, is equal to |α|. It means that one should multiply all points of the vertical axis (y-coordinates) in the graph by the value of α.
Period
For y = cot (x), the period is equal to π. It ways that ane cycle of a cotangent graph occurs between 0 and π. The menstruation of y = cot βx is equal to π/β. For y = α cot (βx - c) + d, the flow is π / |β|.
Domain
Ordered pairs of the form (x, cot x) make upwardly the cotangent function. Since cot (x) = cos (x) / sin (x), the domain of the cotangent office is the set up of existent numbers, except those values of southward for which sin (x) = 0. Hence the domain contains all elements x such that 10 ≠ nπ, where n is an integer. For the domain of the graph y = α cot (βx), the domain is x ≠ π/|β|k. For the cotangent role of format y = α cot (βx - c) + d, the domain is x ≠ c/β + π/|β|k, where k is an integer.
Range
The range of the cotangent function is all real numbers. For the graph y = α cot (βx), it is (-∞, ∞) and for y = α cot (βx - c) + d, the range of the cotangent function with this organisation is (-∞, -|α|] U [|α|, ∞).
Continuity
Each function is discontinuous at values of ten, for which its reciprocal is cipher. In the cotangent function'south case, it is not continuous at values of x, for which tangent is zero. The y = cot (x) graph is erratic at nπ, where n is an integer.
Vertical Asymptotes
Scroll to Go on
Read More From Owlcation
Like the usual graph of inverse functions, the cotangent function has vertical asymptotes at the terminate of one bicycle. The vertical asymptotes for the graph y = α cot (βx) occur at x = nπ / |β|, where north is an integer. On the other manus, for y = α cot (βx - c) + d, the vertical asymptotes occur at x = c/β + nπ/|β|, where n is an integer. Note that the vertical asymptotes of a cotangent function are where the denominator of the cot (10) has a value of zero.
X-intercepts
The asymptotes of y = tan (x) are the x-intercepts of the graph y = cot (x). On the other hand, the x-intercepts of y = tan (x) are the asymptotes of y = cot (x).
Vertical Shift
The vertical shift of a cotangent role with equation y = α cot (βx - c) + d is equal to d moving upwardly. Otherwise, if the d is negative, then it shifts downward.
Horizontal Shift
The horizontal shift or the phase shift of a cotangent graph is equal to c/β, where positive results mean the graph shifts to the left and vice versa. For instance, given y = α cot (βx - c) + d, equate the terms inside the parenthesis to zero.
βx - c = 0
10 = c/β
How to Graph a Cotangent Part
As you can discover, the equation y = cot (x) graph is the opposite of the graph of its corresponding role, tangent. When doing the graphs of cotangent functions, do not become overwhelmed and try to compute and plot many points. Y'all need to know where the graph is nix, where it is equal to ane, the location of the vertical asymptotes, and place if there are horizontal and vertical shifts.
Note that there are various forms of cotangent functions. It can be of the form y = α cot (βx) or the grade y = α cot (βx - c) + d with vertical and horizontal shifts. We can graph cotangent functions by following the step-by-stride procedure shown beneath.
- Express the role in the simplest form f(x) = α cot (βx + c) + d.
- Determine the fundamental properties. Identify the parameters, including the stretching gene/amplitude, menses, horizontal and vertical shifts, etc.
- Notice the vertical asymptotes.
- Find the values for the domain and range.
- Determine the x-intercepts. It is good preparation for plotting reference points.
- Identify the vertical and horizontal shifts, if at that place are any.
- Evaluate and graph the cotangent office.
Instance 1: Graphing a Unproblematic Cotangent Function
Determine the parameters of the cotangent equation y = 4cot (4x).
Solution
The given cotangent function is already in the y = α cot (βx). Next, identify the key properties or parameters needed to graph the cotangent function like amplitude, period, etc.
Amplitude: The coefficient 4 is the amplitude of y = 4cot (4x).
Aamplitude = |α|
Amplitude = |4|
Period: Solve for the period of y = 4cot (4x) using the formula P = π / |β|. We can identify that the value of β from the given equation is equal to 4.
P = π / |β|
P = π / |4|
P = π / 4
Domain: The domain of a cotangent function is the set of input or statement values for which information technology is defined and accurate.
πn / four < x < π / iv + πn / four
Vertical Asymptotes: Solve for the vertical asymptotes of the cotangent function using the general formula. The result shown below ways that the one vertical asymptote appears at π / iv and occurs every P = π / 4.
x = c/β + nπ/|β|
ten = 0 + nπ / 4
x = nπ / four
X-intercepts: Adjacent, plot reference points of the graph by getting the x-intercepts. Substitute y = 0 to the given cotangent equation.
At y = 0,
y = 4 cot (4x)
0 = 4 cot (4(x))
x = π/8 + πn/4
Where due north is any integer
At northward =0, x = π/viii
y = iv cot (4x)
y = 4 cot (4(π/8))
y = 0
At north = i, x = 3π/8
y = 4 cot (4x)
y = 4 cot (iv(3π/8))
y = 0
At due north = -1, x = -π/8
y = 4 cot (4x)
y = 4 cot (4(-π/8))
y = 0
You can observe that the value of y is naught for x with values π/viii + πn/iv. Therefore, the axis interception points occur at (π/eight + πn/4, 0), where n is an integer.
Finally, sketch the graph of the given function given the period is π / four, 1 of the vertical asymptotes is π / four, y = 0 when x = π/8, x = -π/8, and ten = 3π/8.
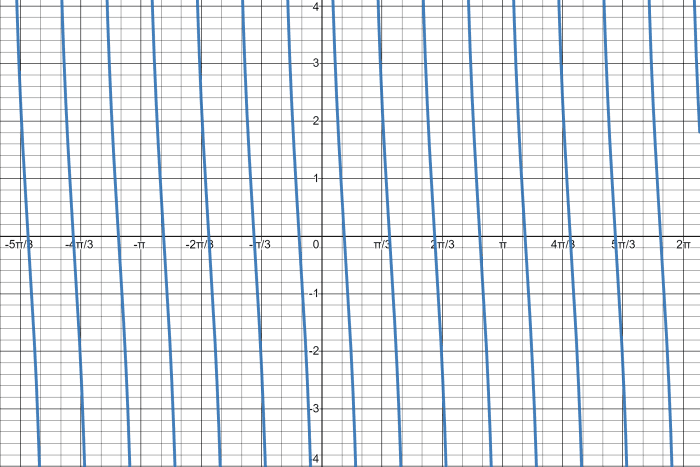
Simple Cotangent Graph
Example two: Cotangent Function with Horizontal and Vertical Shift
Sketch the cotangent graph of the equation y = 5cot (πx/8 - π/two) + three.
Solution
The given cotangent equation has both stage shift and vertical shift. The beginning step is to identify the critical properties of the given cotangent equation to sketch its graph.
Amplitude: The coefficient v is the amplitude of y = 5cot (πx/8 - π/ii) + 3. Therefore, the stretching cistron is five.
Aamplitude = |α|
Amplitude = |5|
Amplitude = 5
Period: Solve for the period of y = 5 cot (πx/8 - π/two) + 3 using the formula P = π / |β|. We can identify that the value of β from the given equation is equal to π/8.
P = π / |β|
P = π / |π/viii|
P = eight
Vertical Asymptotes: Solve for the vertical asymptotes of the cotangent office using the general formula.
x = c/β + nπ/|β|
x = (-π/ii) / (π/8) + nπ / (π/viii)
x = -iv + 8n
Horizontal Shift: The graph shifts 4 units to the right.
Phase shift = c/β
Phase shift = -π/2 / (π/8)
Phase shift = -4
Vertical Shift: The vertical shift of the cotangent equation y = 5cot (πx/8 - π/2) + iii equals three units that shift upwards.
Inflection Points: Find the inflection points to run into where some of the graph's points are plotted in the cartesian coordinate system.
At y = 0
0 = v cot (πx/8 - π/2) + 3
x = ix.376 + 8n
x = 17.376 + 8n
At n = 1
x = nine.376 + 8(1)
10 = 17.376
At n = -one
10 = 9.376 + viii(-one)
x = i.376
At due north = -2
ten = ix.376 + 8(-two)
ten = -6.624
Finally, sketch the graph of the cotangent equation with both phase shift and vertical shift.
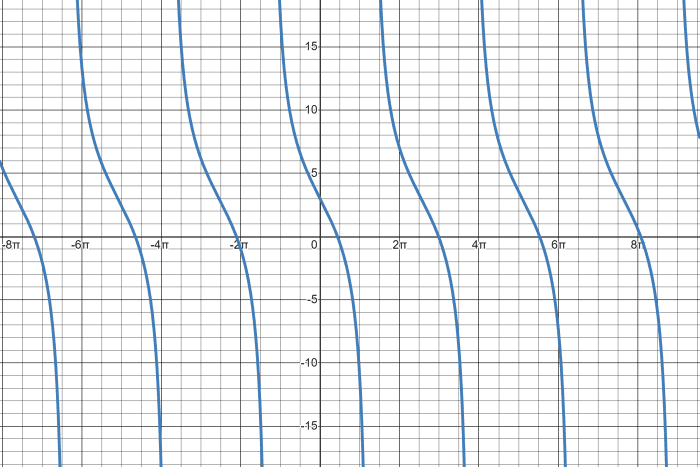
Cotangent Graph with Horizontal and Vertical Shifts
Instance 3: Sketching a Cotangent Function with Phase Shift
Draw the cotangent graph of the equation y = -3cot (x/2 + π/three).
Solution
The given cotangent function is already in the y = α cot (βx + c). Place the parameters needed to graph the cotangent equation.
Amplitude: The coefficient -3 is the amplitude of y = -3 cot (ten/2 + π/3).
Amplitude = |α|
Amplitude = |-3|
Amplitude = 3
Menstruation: Solve for the catamenia of y =-3 cot (x/2 + π/3) using the formula P = π / |β|. We can place that the value of β from the given equation is equal to 1/2.
P = π / |β|
P = π / |1/2|
P = 2π
Domain: The domain of a cotangent function is the fix of input or argument values for which the part is defined and existent. The domain of y = -3 cot (10/2 + π/3) is shown below.
2πn ≤ ten < 4π/3 + 2πn
Vertical Asymptotes: Solve for the vertical asymptotes of the cotangent role using the formula. From the result shown below, the vertical asymptote appears at 2π/3 + 2πn.
ten = c/β + nπ/|β|
x = (π/3) / (½) + nπ / (½)
ten = 2π/iii + 2πn
Ten-intercepts: All inflection points are in a domain and non on domain edges.
At y =0
y = -3 cot (ten/2 + π/3)
0 = -3 cot (10/two + π/3)
x = π/3 + 2πn
At n = 1
x = π/3 + 2π(1)
x = 7π/3
At n = -1
ten = π/3 + 2π(-1)
x = -5π/3
Horizontal Shift/Phase Shift: There is a horizontal shift in the cotangent graph since there is a constant added within the grouping symbols of the function. Use the formula for horizontal shift c/β. Since the resulting value for phase shift is positive, the graph shifts horizontally to the right.
Phase shift = -c/β
Phase shift = -π/3 / (½)
Phase shift = -2π/3
Or
βx + c = 0
x/two + π/3 = 0
x = -2π/3
Finally, sketch the cotangent graph using the obtained parameters with a horizontal shift of 2π/3 to the right.
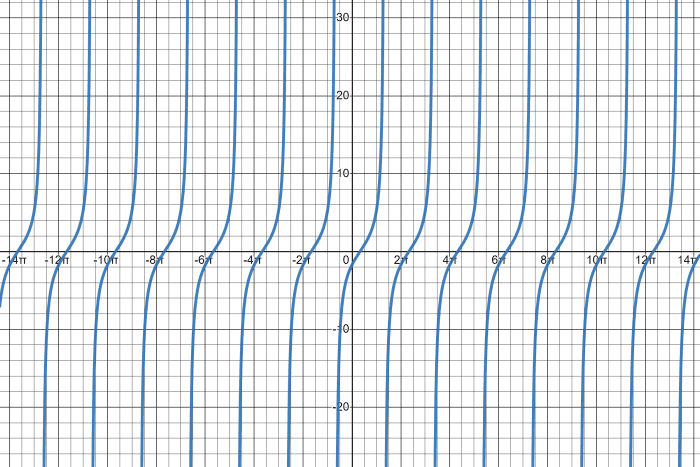
Cotangent Graph with Phase Shift
Case four: Graphing a Cotangent Function with a Stretch Cistron
Graph the cotangent part y = 4 cot (⅕ x).
Solution
Describe the transformation of the cotangent office y = 4cot (⅕ x) and and then graph it. Identify the parameters such as the stretch factor, period, domain, etc.
Amplitude: The coefficient four is the amplitude of y = 4cot (⅕ 10). Therefore the given office has a stretch factor of 4.
Aamplitude = |α|
Amplitude = |4|
Amplitude = 4
Flow: Solve for the menses of y = 4cot (⅕ x) using the formula P = π / |β|. We tin can place that the value of β from the given equation is equal to ⅕.
P = π / |β|
P = π / |⅕|
P = 5π
Domain: The domain of a cotangent function is the prepare of input or argument values for which it is defined and accurate.
5πn < x < 5π + 5π
Vertical Asymptotes: Solve for the vertical asymptotes of the cotangent function using the formula. From the upshot shown beneath, the vertical asymptotes appear at every 10 = 5πn.
x = c/β + nπ/|β|
10 = 0 + nπ / |⅕|
x = 5πn
X-intercepts: Find the x-intercepts of the graph to plot other essential points of the cotangent graph.
At y = 0,
0 = four cot (⅕ x)
y = 4 cot (⅕ 10)
x = 5π/2 + 5πn
At n = i,
x = 5π/ii + 5π(1)
x = 15π/2
At northward = -1
x = 5π/2 + 5π(-ane)
x = - 5π/2
Lastly, sketch the cotangent graph applying the obtained parameters, especially the stretch cistron.
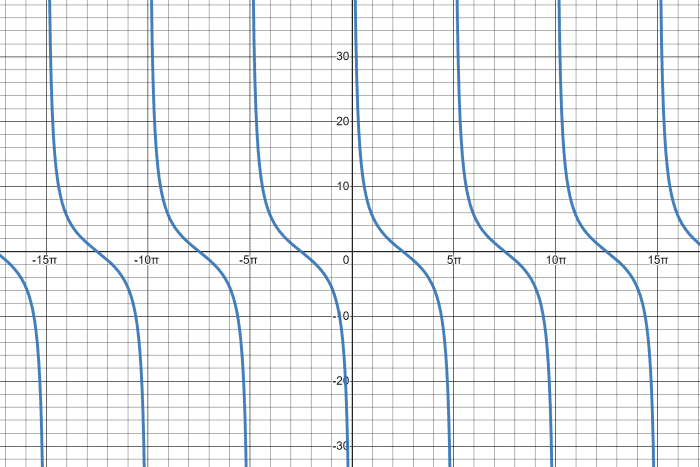
Cotangent Graph with Stretch Factor
Example 5: Graphing a Cotangent Role with Phase Shift
Sketch the graph y = cot (5x - π/two).
Solution
Locate the essential parameters such as period, horizontal shift, and vertical asymptotes needed to graph the given cotangent function.
Period: Solve for the menses of y = 4cot (⅕ 10) using the formula P = π / |β|. We tin can place that the value of β from the given equation is equal to ⅕.
P = π / |β|
P = π / |5||
P = π / 5
Vertical Asymptotes: Solve for the vertical asymptotes of the cotangent function using the formula. From the upshot shown below, the vertical asymptotes appear at every x = 5πn.
10 = c/β + nπ/|β|
10 = -π/2 / 5 + nπ / |5|
ten = -π/x + nπ/five
Horizontal Shift: Equate the terms within the parenthesis to zero and solve for the value of x, which represents the horizontal shift of the cotangent equation. With the positive event, the phase shifts to the left direction.
5x - π/2 = 0
x = π/ii / 5
x = π/10
Lastly, sketch the cotangent graph.
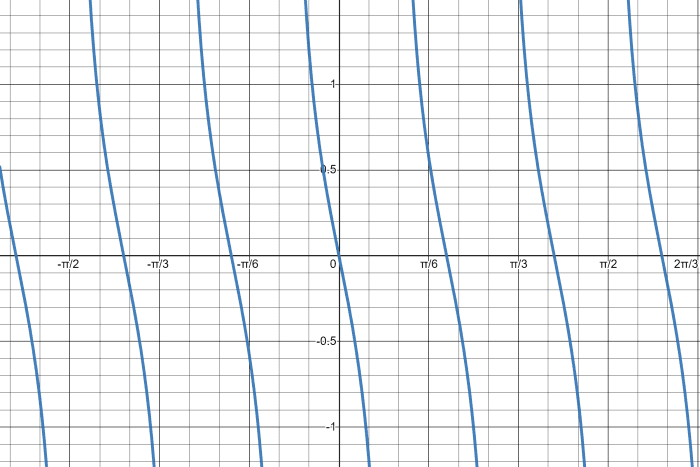
Graphing a Cotangent Function with Phase Shift
Explore More Articles Virtually Graphs
- Secant Graph: How to Graph a Secant Office
Learn how to sketch a secant graph by learning its properties such every bit period, horizontal shift, vertical shift, aamplitude, and more than. This article also includes examples of step-by-step procedures on how to graph secant functions with unlike nature - How to Graph an Ellipse Given an Equation
Learn how to graph an ellipse given the general form and standard form. Know the dissimilar elements, properties, and formulas necessary in solving bug about ellipse. - How to Graph a Circle Given a General or Standard Equation
Learn how to graph a circle given the general form and standard form. Familiarize with converting general grade to standard class equation of a circle and know the formulas necessary in solving problems most circles.
This content is authentic and true to the best of the author's knowledge and is not meant to substitute for formal and individualized communication from a qualified professional.
© 2021 Ray
Period Of A Cot Function,
Source: https://owlcation.com/stem/Cotangent-Graph-How-to-Graph-a-Cotangent-Function
Posted by: robinsonweir1970.blogspot.com


0 Response to "Period Of A Cot Function"
Post a Comment