Domain Of The Cosine Function
Skip to chief content
Domain and Range of Trigonometric Functions
The domain of a function is the specific fix of values that the independent variable in a function can take on. The range is the resulting values that the dependant variable tin take equally x varies throughout the domain.
Domain and range for sine and cosine functions
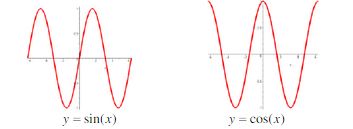
There are no restrictions on the domain of sine and cosine functions; therefore, their domain is such that x ∈ R. Notice, however, that the range for both y = sin(x) and y = cos(ten) is between -one and one. Therefore, transformations of these functions in the form of shifts and stretches will affect the range only not the domain.
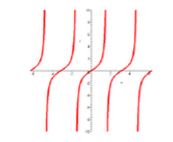
The domain and range for tangent functions
Notice that y = tan(x) has vertical asymptotes at . Therefore, its domain is such that
. However, its range is such at y ∈ R, because the function takes on all values of y. In this case, transformations volition touch the domain but not the range.
Instance: Find the domain and range of y = cos(x) – iii
Solution:
Domain: x ∈ R
Range: - 4 ≤ y ≤ - two, y ∈ R
Find that the range is simply shifted downward 3 units.
Example: Find the domain and range of y = iii tan(x)
Solution:
Domain: , x ∈ R
Notice that the domain is the same equally the domain for y = tan(ten) because the graph was stretched vertically—which does non alter where the vertical asymptotes occur.
Range: y ∈ R
Example 1:
Case 2:
Domain Of The Cosine Function,
Source: https://nool.ontariotechu.ca/mathematics/functions/domain-range/domain-and-range-of-trigonometric-functions.php
Posted by: robinsonweir1970.blogspot.com


0 Response to "Domain Of The Cosine Function"
Post a Comment