Frequency Of Oscillation Lc Circuit

Electric "resonator" circuit, consisting of inductive and capacitive elements with no resistance

LC circuit (left) consisting of ferrite coil and capacitor used as a tuned circuit in the receiver for a radio clock

An LC circuit, besides called a resonant circuit, tank circuit, or tuned circuit, is an electric circuit consisting of an inductor, represented by the alphabetic character Fifty, and a capacitor, represented by the letter C, connected together. The circuit can human activity every bit an electrical resonator, an electrical analogue of a tuning fork, storing energy oscillating at the circuit's resonant frequency.

LC circuits are used either for generating signals at a particular frequency, or picking out a point at a item frequency from a more than circuitous signal; this office is chosen a bandpass filter. They are key components in many electronic devices, particularly radio equipment, used in circuits such as oscillators, filters, tuners and frequency mixers.

An LC circuit is an arcadian model since it assumes there is no dissipation of free energy due to resistance. Any practical implementation of an LC excursion will always include loss resulting from pocket-size simply non-zero resistance within the components and connecting wires. The purpose of an LC circuit is usually to oscillate with minimal damping, and so the resistance is fabricated as depression equally possible. While no practical circuit is without losses, it is nonetheless instructive to study this ideal form of the circuit to gain understanding and physical intuition. For a circuit model incorporating resistance, see RLC excursion.

Terminology [edit]

The two-element LC excursion described above is the simplest blazon of inductor-capacitor network (or LC network). Information technology is also referred to equally a 2d order LC circuit to distinguish information technology from more complicated (higher club) LC networks with more inductors and capacitors. Such LC networks with more than ii reactances may accept more than than ane resonant frequency.

The order of the network is the guild of the rational function describing the network in the circuitous frequency variable s. Mostly, the club is equal to the number of L and C elements in the circuit and in any event cannot exceed this number.

Operation [edit]

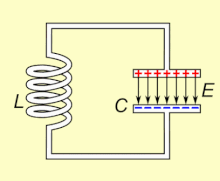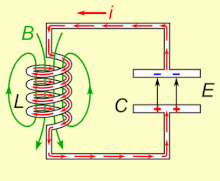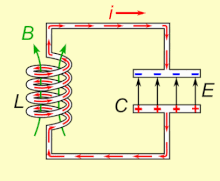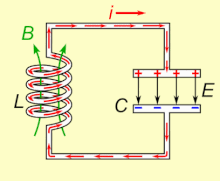
Animated diagram showing the operation of a tuned circuit (LC excursion). The capacitor C stores energy in its electrical field E and the inductor L stores energy in its magnetic field B (dark-green). The animation shows the circuit at progressive points in the oscillation. The oscillations are slowed down; in an actual tuned excursion the charge may oscillate back and forth thousands to billions of times per second.

An LC excursion, oscillating at its natural resonant frequency, can store electrical energy. See the animation. A capacitor stores energy in the electric field (E) between its plates, depending on the voltage across it, and an inductor stores free energy in its magnetic field (B), depending on the current through it.

If an inductor is connected beyond a charged capacitor, the voltage beyond the capacitor will drive a current through the inductor, building up a magnetic field effectually information technology. The voltage beyond the capacitor falls to zero as the charge is used up by the electric current flow. At this point, the energy stored in the roll'due south magnetic field induces a voltage across the curl, because inductors oppose changes in current. This induced voltage causes a current to begin to recharge the capacitor with a voltage of opposite polarity to its original charge. Due to Faraday's police, the EMF which drives the electric current is caused by a subtract in the magnetic field, thus the energy required to charge the capacitor is extracted from the magnetic field. When the magnetic field is completely dissipated the current will end and the accuse will over again be stored in the capacitor, with the opposite polarity as before. And then the bike will begin again, with the current flowing in the opposite direction through the inductor.

The accuse flows back and forth between the plates of the capacitor, through the inductor. The energy oscillates dorsum and along betwixt the capacitor and the inductor until (if not replenished from an external excursion) internal resistance makes the oscillations die out. The tuned excursion'southward action, known mathematically every bit a harmonic oscillator, is similar to a pendulum swinging back and forth, or water sloshing dorsum and forth in a tank; for this reason the circuit is also chosen a tank circuit.^[1] The natural frequency (that is, the frequency at which it will oscillate when isolated from whatever other system, as described to a higher place) is determined by the capacitance and inductance values. In near applications the tuned circuit is part of a larger circuit which applies alternate current to information technology, driving continuous oscillations. If the frequency of the applied current is the circuit'due south natural resonant frequency (natural frequency ${\displaystyle f_{0}\,}$ below ), resonance will occur, and a pocket-size driving electric current tin excite large amplitude oscillating voltages and currents. In typical tuned circuits in electronic equipment the oscillations are very fast, from thousands to billions of times per second.^{[ citation needed ]}

Resonance outcome [edit]

Resonance occurs when an LC excursion is driven from an external source at an angular frequency ω ₀ at which the anterior and capacitive reactances are equal in magnitude. The frequency at which this equality holds for the particular circuit is chosen the resonant frequency. The resonant frequency of the LC excursion is

${\displaystyle \omega _{0}={\frac {i}{\sqrt {LC}}},}$

where L is the inductance in henries, and C is the capacitance in farads. The athwart frequency ω ₀ has units of radians per second.

The equivalent frequency in units of hertz is

${\displaystyle f_{0}={\frac {\omega _{0}}{2\pi }}={\frac {one}{ii\pi {\sqrt {LC}}}}.}$

Applications [edit]

The resonance event of the LC circuit has many of import applications in signal processing and communications systems.

• The about mutual application of tank circuits is tuning radio transmitters and receivers. For example, when tuning a radio to a item station, the LC circuits are set at resonance for that item carrier frequency.
• A serial resonant circuit provides voltage magnification.
• A parallel resonant circuit provides current magnification.
• A parallel resonant circuit can exist used as load impedance in output circuits of RF amplifiers. Due to high impedance, the gain of amplifier is maximum at resonant frequency.
• Both parallel and series resonant circuits are used in consecration heating.

LC circuits behave as electronic resonators, which are a fundamental component in many applications:

• Amplifiers
• Oscillators
• Filters
• Tuners
• Mixers
• Foster–Seeley discriminator
• Contactless cards
• Graphics tablets
• Electronic article surveillance (security tags)

Time domain solution [edit]

Kirchhoff'southward laws [edit]

Past Kirchhoff's voltage police force, the voltage 5_C across the capacitor plus the voltage V_L beyond the inductor must equal zero:

${\displaystyle V_{C}+V_{L}=0.}$

Too, by Kirchhoff'due south electric current law, the current through the capacitor equals the electric current through the inductor:

${\displaystyle I_{C}=I_{50}.}$

From the constitutive relations for the excursion elements, we also know that

${\displaystyle {\brainstorm{aligned}V_{L}(t)&=L{\frac {\mathrm {d} I_{50}}{\mathrm {d} t}},\\I_{C}(t)&=C{\frac {\mathrm {d} V_{C}}{\mathrm {d} t}}.\end{aligned}}}$

Differential equation [edit]

Rearranging and substituting gives the second order differential equation

${\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}I(t)+{\frac {1}{LC}}I(t)=0.}$

The parameter ω ₀ , the resonant angular frequency, is divers as

${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}}.}$

Using this can simplify the differential equation:

${\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}I(t)+\omega _{0}^{ii}I(t)=0.}$

The associated Laplace transform is

${\displaystyle s^{2}+\omega _{0}^{two}=0,}$

thus

${\displaystyle southward=\pm j\omega _{0},}$

where j is the imaginary unit.

Solution [edit]

Thus, the complete solution to the differential equation is

${\displaystyle I(t)=Ae^{+j\omega _{0}t}+Be^{-j\omega _{0}t}}$

and can be solved for A and B by considering the initial conditions. Since the exponential is complex, the solution represents a sinusoidal alternating current. Since the electrical current I is a concrete quantity, it must be real-valued. As a consequence, it tin can be shown that the constants A and B must be complex conjugates:

${\displaystyle A=B^{*}.}$

Now allow

${\displaystyle A={\frac {I_{0}}{2}}e^{+j\phi }.}$

Therefore,

${\displaystyle B={\frac {I_{0}}{2}}east^{-j\phi }.}$

Next, we can use Euler's formula to obtain a real sinusoid with amplitude I ₀ , athwart frequency ω ₀ = 1 / √ LC , and stage angle ${\displaystyle \phi }$ .

Thus, the resulting solution becomes

${\displaystyle I(t)=I_{0}\cos \left(\omega _{0}t+\phi \right),}$

${\displaystyle 5(t)=L{\frac {\mathrm {d} I}{\mathrm {d} t}}=-\omega _{0}LI_{0}\sin \left(\omega _{0}t+\phi \right).}$

Initial conditions [edit]

The initial conditions that would satisfy this result are

${\displaystyle I(0)=I_{0}\cos \phi ,}$

${\displaystyle V(0)=L{\frac {\mathrm {d} I}{\mathrm {d} t}}{\Bigg |}_{t=0}=-\omega _{0}LI_{0}\sin \phi .}$

Series circuit [edit]

In the series configuration of the LC excursion, the inductor (L) and capacitor (C) are connected in series, as shown hither. The total voltage V across the open terminals is simply the sum of the voltage beyond the inductor and the voltage across the capacitor. The current I into the positive terminal of the excursion is equal to the current through both the capacitor and the inductor.

${\displaystyle {\brainstorm{aligned}V&=V_{Fifty}+V_{C},\\I&=I_{Fifty}=I_{C}.\stop{aligned}}}$

Resonance [edit]

Anterior reactance magnitude X_L increases every bit frequency increases, while capacitive reactance magnitude 10_C decreases with the increase in frequency. At one item frequency, these two reactances are equal in magnitude just opposite in sign; that frequency is chosen the resonant frequency f ₀ for the given circuit.

Hence, at resonance,

${\displaystyle {\begin{aligned}X_{Fifty}&=X_{C},\\\omega L&={\frac {1}{\omega C}}.\end{aligned}}}$

Solving for ω, nosotros accept

${\displaystyle \omega =\omega _{0}={\frac {i}{\sqrt {LC}}},}$

which is defined as the resonant angular frequency of the excursion. Converting angular frequency (in radians per second) into frequency (in hertz), 1 has

${\displaystyle f_{0}={\frac {\omega _{0}}{2\pi }}={\frac {1}{2\pi {\sqrt {LC}}}}.}$

In a series configuration, X_C and 10_L cancel each other out. In existent, rather than idealised, components, the current is opposed, more often than not by the resistance of the coil windings. Thus, the current supplied to a series resonant circuit is maximal at resonance.

• In the limit as f → f ₀ current is maximal. Excursion impedance is minimal. In this land, a circuit is called an acceptor circuit ^[ii]
• For f < f ₀ , X_L ≪ −X_C . Hence, the circuit is capacitive.
• For f > f ₀ , X_L ≫ −X_C . Hence, the circuit is inductive.

Impedance [edit]

In the series configuration, resonance occurs when the complex electrical impedance of the circuit approaches zero.

Starting time consider the impedance of the serial LC circuit. The total impedance is given by the sum of the anterior and capacitive impedances:

${\displaystyle Z=Z_{L}+Z_{C}\;.}$

Writing the anterior impedance as Z₅₀ = jωL and capacitive impedance as Z_C = 1 / jωC and substituting gives

${\displaystyle Z(\omega )=j\omega L+{\frac {1}{j\omega C}}\;.}$

Writing this expression under a common denominator gives

${\displaystyle Z(\omega )=j\left({\frac {\omega ^{2}LC-1}{\omega C}}\right)\;.}$

Finally, defining the natural angular frequency as

${\displaystyle \omega _{0}={\frac {one}{\sqrt {LC\,}}}\,,}$

the impedance becomes

${\displaystyle Z(\omega )=j\ L\ \left({\frac {\omega ^{2}-\omega _{0}^{2}}{\omega }}\right)=j\ \omega _{0}L\ \left({\frac {\omega }{\omega _{0}}}-{\frac {\omega _{0}}{\omega }}\right)\,,}$

where ${\displaystyle \,\omega _{0}L\ \,}$ gives the reactance of the inductor at resonance.

The numerator implies that in the limit as ω → ±ω ₀ , the full impedance Z will exist zero and otherwise not-nix. Therefore the series LC excursion, when connected in series with a load, will act every bit a band-pass filter having goose egg impedance at the resonant frequency of the LC circuit.

Parallel excursion [edit]

When the inductor (L) and capacitor (C) are continued in parallel as shown here, the voltage V across the open terminals is equal to both the voltage across the inductor and the voltage across the capacitor. The total current I flowing into the positive terminal of the circuit is equal to the sum of the current flowing through the inductor and the current flowing through the capacitor:

${\displaystyle {\begin{aligned}V&=V_{L}=V_{C},\\I&=I_{L}+I_{C}.\cease{aligned}}}$

Resonance [edit]

When X_L equals X_C , the two co-operative currents are equal and opposite. They cancel out each other to give minimal electric current in the main line (in principle, naught current). Even so, there is a large current circulating betwixt the capacitor and inductor. In principle, this circulating current is infinite, but in reality is limited by resistance in the excursion, particularly resistance in the inductor windings. Since total current is minimal, in this state the full impedance is maximal.

The resonant frequency is given by

${\displaystyle f_{0}={\frac {\omega _{0}}{two\pi }}={\frac {1}{2\pi {\sqrt {LC}}}}.}$

Note that whatever co-operative current is not minimal at resonance, but each is given separately by dividing source voltage (Five) by reactance (Z). Hence I = 5 / Z , as per Ohm's law.

• At f ₀ , the line current is minimal. The total impedance is maximal. In this state a excursion is called a rejector circuit.^[3]
• Below f ₀ , the excursion is anterior.
• Above f ₀ , the excursion is capacitive.

Impedance [edit]

The same analysis may be applied to the parallel LC excursion. The total impedance is and then given by

${\displaystyle Z={\frac {Z_{L}Z_{C}}{Z_{50}+Z_{C}}},}$

and afterwards commutation of Z_L = jωL and Z_C = 1 / jωC and simplification, gives

${\displaystyle Z(\omega )=-j\cdot {\frac {\omega L}{\omega ^{ii}LC-1}}.}$

Using

${\displaystyle \omega _{0}={\frac {one}{\sqrt {LC}}},}$

it further simplifies to

${\displaystyle Z(\omega )=-j\left({\frac {1}{C}}\right)\left({\frac {\omega }{\omega ^{two}-\omega _{0}^{2}}}\right).}$

Note that

${\displaystyle \lim _{\omega \to \omega _{0}}Z(\omega )=\infty ,}$

just for all other values of ω the impedance is finite.

Thus, the parallel LC circuit connected in series with a load will act as band-stop filter having infinite impedance at the resonant frequency of the LC circuit, while the parallel LC circuit connected in parallel with a load will deed equally band-laissez passer filter.

Laplace solution [edit]

The LC excursion tin exist solved using the Laplace transform.

We begin by defining the relation between current and voltage across the capacitor and inductor in the usual manner:

${\displaystyle v_{\mathrm {C} }(t)=5(t)\ ,~}$ ${\displaystyle i(t)=C\ {\frac {\mathrm {d} \ v_{\mathrm {C} }}{\mathrm {d} t}}\ ,~}$ and ${\displaystyle ~v_{\mathrm {L} }(t)=L\ {\frac {\mathrm {d} \ i}{\mathrm {d} t}}\;.}$

Then by awarding of Kirchoff'southward laws, we may make it at the system'southward governing differential equations

${\displaystyle v_{in}(t)=v_{\mathrm {50} }(t)+v_{\mathrm {C} }(t)=L\ {\frac {\mathrm {d} \ i}{\mathrm {d} t}}+v=L\ C\ {\frac {\mathrm {d} ^{2}\ v}{\mathrm {d} t^{two}}}+five\;.}$

With initial conditions ${\displaystyle \ v(0)=v_{0}\ }$ and ${\displaystyle \ i(0)=i_{0}=C\cdot v'(0)=C\cdot v'_{0}\;.}$

Making the post-obit definitions,

${\displaystyle \omega _{0}\equiv {\frac {ane}{\ {\sqrt {L\ C\ }}}}~}$ and ${\displaystyle ~f(t)\equiv \omega _{0}^{2}\ v_{\mathrm {in} }(t)}$

gives

${\displaystyle f(t)={\frac {\ \mathrm {d} ^{2}\ 5\ }{\mathrm {d} t^{2}}}+\omega _{0}^{2}\ v\;.}$

Now we utilise the Laplace transform.

${\displaystyle \operatorname {\mathcal {L}} \left[\ f(t)\ \right]=\operatorname {\mathcal {L}} \left[\ {\frac {\ \mathrm {d} ^{2}\ five\ }{\mathrm {d} t^{two}}}+\omega _{0}^{2}\ 5\ \correct]\,,}$

${\displaystyle F(due south)=s^{2}\ V(south)-south\ v_{0}-v'_{0}+\omega _{0}^{2}\ V(due south)\;.}$

The Laplace transform has turned our differential equation into an algebraic equation. Solving for 5 in the southward domain (frequency domain) is much simpler viz.

${\displaystyle V(south)={\frac {\ s\ v_{0}+5'_{0}+F(due south)\ }{s^{ii}+\omega _{0}^{2}}}\,,}$

which can be transformed back to the fourth dimension domain via the changed Laplace transform:

${\displaystyle five(t)=v_{0}\cos(\omega _{0}\ t)+{\frac {v'_{0}}{\ \omega _{0}\ }}\ \sin(\omega _{0}\ t)+\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {F(s)}{\ s^{2}+\omega _{0}^{two}\ }}\ \right]}$

The last term is dependent on the exact grade of the input voltage. Two common cases are the Heaviside step function and a sine wave. For a Heaviside step function we become

${\displaystyle v_{\mathrm {in} }(t)=M\ u(t)\,,}$

${\displaystyle \operatorname {\mathcal {L}} ^{-i}\left[\ \omega _{0}^{2}{\frac {V_{\mathrm {in} }(southward)}{\ s^{two}+\omega _{0}^{two}\ }}\ \right]~=~\operatorname {\mathcal {L}} ^{-ane}\left[\ \omega _{0}^{2}\ M\ {\frac {1}{\ s\ (due south^{2}+\omega _{0}^{2})\ }}\ \right]~=~M\ {\Bigl (}one-\cos(\omega _{0}\ t){\Bigr )}\,,}$

${\displaystyle v(t)=v_{0}\ \cos(\omega _{0}\ t)+{\frac {five'_{0}}{\omega _{0}}}\ \sin(\omega _{0}\ t)+G\ {\Bigl (}ane-\cos(\omega _{0}\ t){\Bigr )}\;.}$

For the case of a sinusoidal function as input nosotros get:

${\displaystyle v_{\mathrm {in} }(t)=U\ \sin(\omega _{\mathrm {f} }\ t)\Rightarrow V_{\mathrm {in} }(due south)={\frac {\ U\ \omega _{\mathrm {f} }\ }{\ s^{two}+\omega _{\mathrm {f} }^{2}\ }}\,,}$

${\displaystyle \operatorname {\mathcal {L}} ^{-i}\left[\ \omega _{0}^{2}\ {\frac {1}{\ s^{two}+\omega _{0}^{ii}\ }}\ {\frac {U\ \omega _{\mathrm {f} }}{\ southward^{ii}+\omega _{\mathrm {f} }^{2}\ }}\ \correct]=\operatorname {\mathcal {L}} ^{-1}\left[\ {\frac {\ \omega _{0}^{2}\ U\omega _{\mathrm {f} }\ }{\ \omega _{\mathrm {f} }^{2}-\omega _{0}^{2}\ }}\left({\frac {ane}{s^{2}+\omega _{0}^{ii}}}-{\frac {1}{\ due south^{2}+\omega _{f}^{ii}\ }}\right)\ \right]\,}$

${\displaystyle \qquad \qquad ={\frac {\ \omega _{0}^{ii}\ U\ \omega _{\mathrm {f} }\ }{\omega _{\mathrm {f} }^{2}-\omega _{0}^{ii}}}\ \left({\frac {1}{\omega _{0}}}\ \sin(\omega _{0}\ t)-{\frac {one}{\ \omega _{\mathrm {f} }\ }}\ \sin(\omega _{\mathrm {f} }\ t)\right)\;,}$ and then

${\displaystyle five(t)=v_{0}\cos(\omega _{0}\ t)+{\frac {v'_{0}\ b}{\ b\ \omega _{0}\ }}\ \sin(\omega _{0}\ t)+{\frac {\omega _{0}^{ii}\ U\ \omega _{\mathrm {f} }}{\ \omega _{\mathrm {f} }^{two}-\omega _{0}^{ii}\ }}\left({\frac {1}{\omega _{0}}}\ \sin(\omega _{0}\ t)-{\frac {1}{\ \omega _{\mathrm {f} }\ }}\ \sin(\omega _{\mathrm {f} }\ t)\right)\;.}$

History [edit]

The first evidence that a capacitor and inductor could produce electrical oscillations was discovered in 1826 by French scientist Felix Savary.^{[4] [5]} He found that when a Leyden jar was discharged through a wire wound around an fe needle, sometimes the needle was left magnetized in one direction and sometimes in the opposite direction. He correctly deduced that this was caused past a damped oscillating discharge current in the wire, which reversed the magnetization of the needle dorsum and forth until it was also small to have an effect, leaving the needle magnetized in a random management. American physicist Joseph Henry repeated Savary's experiment in 1842 and came to the aforementioned conclusion, apparently independently.^{[6] [seven]}

Irish gaelic scientist William Thomson (Lord Kelvin) in 1853 showed mathematically that the belch of a Leyden jar through an inductance should be oscillatory, and derived its resonant frequency.^{[4] [vi] [7]} British radio researcher Oliver Lodge, by discharging a large battery of Leyden jars through a long wire, created a tuned circuit with its resonant frequency in the audio range, which produced a musical tone from the spark when it was discharged.^[6] In 1857, German physicist Berend Wilhelm Feddersen photographed the spark produced past a resonant Leyden jar circuit in a rotating mirror, providing visible evidence of the oscillations.^{[iv] [half-dozen] [seven]} In 1868, Scottish physicist James Clerk Maxwell calculated the effect of applying an alternate current to a circuit with inductance and capacitance, showing that the response is maximum at the resonant frequency.^[four] The get-go case of an electric resonance curve was published in 1887 by German physicist Heinrich Hertz in his pioneering paper on the discovery of radio waves, showing the length of spark obtainable from his spark-gap LC resonator detectors as a part of frequency.^[4]

One of the first demonstrations of resonance between tuned circuits was Lodge's "syntonic jars" experiment around 1889.^{[four] [6]} He placed two resonant circuits next to each other, each consisting of a Leyden jar connected to an adjustable 1-turn coil with a spark gap. When a high voltage from an consecration ringlet was practical to ane tuned circuit, creating sparks and thus oscillating currents, sparks were excited in the other tuned circuit only when the circuits were adjusted to resonance. Gild and some English scientists preferred the term "syntony" for this effect, just the term "resonance" eventually stuck.^[iv] The kickoff practical use for LC circuits was in the 1890s in spark-gap radio transmitters to allow the receiver and transmitter to be tuned to the same frequency. The start patent for a radio system that immune tuning was filed by Lodge in 1897, although the commencement practical systems were invented in 1900 past Italian radio pioneer Guglielmo Marconi.^[4]

See besides [edit]

• RL excursion
• RC circuit
• RLC excursion

References [edit]

1. ^ Rao, B. Visvesvara; et al. (2012). Electronic Excursion Analysis. India: Pearson Education Bharat. p. xiii.6. ISBN978-9332511743.
2. ^ What is Acceptor Excursion.
3. ^ "rejector circuit". Oxford Dictionaries. English. Archived from the original on September twenty, 2018. Retrieved 2018-09-twenty .
4. ^ ^{a b c d e f chiliad h} Blanchard, Julian (Oct 1941). "The History of Electrical Resonance". Bell System Technical Periodical. U.S.: American Telephone & Telegraph Co. 20 (four): 415–433. doi:x.1002/j.1538-7305.1941.tb03608.x. S2CID 51669988. Retrieved 2011-03-29 .
5. ^ Savary, Felix (1827). "Memoirs sur l'Aimentation". Annales de Chimie et de Physique. Paris: Masson. 34: 5–37.
6. ^ ^{a b c d eastward} Kimball, Arthur Lalanne (1917). A Higher Text-book of Physics (2nd ed.). New York: Henry Hold. pp. 516–517.
7. ^ ^{a b c} Huurdeman, Anton A. (2003). The Worldwide History of Telecommunications. U.S.: Wiley-IEEE. pp. 199–200. ISBN0-471-20505-2.

External links [edit]

• An electric pendulum by Tony Kuphaldt is a classical story well-nigh the functioning of LC tank
• How the parallel-LC circuit stores free energy is another splendid LC resource.

Frequency Of Oscillation Lc Circuit,

Source: https://en.wikipedia.org/wiki/LC_circuit

Posted by: robinsonweir1970.blogspot.com

Share this post